√99以上 y=x^2 2x-8 domain 173710-Y=x^2+2x-8 domain

1F2 10Find the derivative of x10(x2 1) 1F3 Find dy/dx for y = x 1/n by implicit differentiation 1F4 Calculate dy/dx for x 1/3 y 1/3 = 1 by implicit differentiationY = 3x 1, y = #x^23x 2#, and y = #x^3# Do you notice that each one of those functions has powers of x that are Whole numbers?At a typical x value Such a line enters D at y = x2 and leaves at y = 2x The integral becomes ZZ D (4x2)dA = Z 2 0 Z 2x x2 (4x2)dydx = Z 2 0 4xy 2yy=2x y=x2 dx = Z 2 0 8x2 4x − 4x3 2x2 dx = Z 2 0 (6x2 −4x3 4x)dx = h 2x3 −x4 2x2 i 2 0 = 8 The example we have just done shows that it is sometimes easier to do it one way than the

Misc 3 Find Domain Of F X X2 2x 1 X2 8x 12

Y=x^2+2x-8 domain

Y=x^2+2x-8 domain-Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!2;2), which is in our domain Checking when x= 0 and x= 3 gives us points we already have

Solved X 2 X F X2 2x 8 Determine The Domain Determine The X Intercept S Determine The V Intercept Determine The Equation S For The Vertical Asymptote S Determine The Approximation Equation Near All X Intercepts Determine

Algebra Find the Domain and Range y=x^28 y = x2 8 y = x 2 8 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval NotationA function may be thought of as a rule which takes each member x of a set and assigns, or maps it to the same value y known at its image x → Function → y A letter such as f, g or h is often used to stand for a functionThe Function which squares a number and adds on a 3, can be written as f(x) = x 2 5The same notion may also be used to show how a function affects particular valuesPopular Problems Algebra Find the Domain and Range f (x)=x^22x8 f (x) = x2 − 2x − 8 f ( x) = x 2 2 x 8 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the

 Explanation y = f (x) is defined for all real values of x, except for any that make the denominator equal zero equating the denominator to zero and solving gives the value that x cannot be solve 2x − 8 = 0 ⇒ x = 4 ← excluded value domain is x ∈ R,x ≠ 4 to find any excluded values in the range, rearrange f (x) making x the subjectIf R = x , y x , y , ∈ W , 2 x y =8, then write the domain and range of RTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `y=sqrt(x^23x2) 1/(sqrt(32xx^2)` find the domain = ?

 5Find the domain of the following function y=x2 x^2 2x −8 Select the appropriate response A) x equals −4, 2 B) x cannot equal −4, 2 C)Not possible to solve7 General solution is y 2 − 1 4 sin2y = x2 2 2xln xC , 8 General solution is siny = e−x2A, and particular solution is siny = e−x2, 9 General solution is y(1 x2)12 = k , and particular solution is y(1x2)12 = 2, 10 General solution is tan−1 y = ln x C, and particular solution is tan−1 y = ln x π 4, 11 General solution isChapter 2 21 Functions definition, notation A function is a rule (correspondence) that assigns to each element x of one set , say X, one and only one element y of another set, Y The set X is called the domain of the function and the set of all elements of the set Y that are associated with some element of the set X is called the range of the function

Domain And Range Examples Domain And Range Of A Function

Solved 4pts 17 Find The Domain Y 2x 5 2 Domain Of An Chegg Com

31 Problem 178 Prove that if n is a perfect square, then n2 is not a perfect square Proof Suppose that n = x2 and n2 = y2, with both x and y nonnegative naturals We know a formula for the difference of squares (n2) (n)= x2 y2 2 =(x y)(x y) Since 2 is a prime number, one of these factors must be 2 and the other must be 1Y=x^2–2x8 y=sqrt (x^2–2x8) The square root function returns complex numbers for any arguments less than one The function x^2–2x8 is negative for the range 2 < x < 4, and so doesn't give any yvalue for this range It gives a positive value everywhere else So the domain of the function consists of x4, a Continue Reading Bnar XetabDomain {—4,0,8} Now put each value of domain in place of x and get the value of y On putting values in x, obtained value of y comes out to be {1,3,7} So option A is the answer to this question I hope that you have got your answer and understood it 😊😉😉😉

Solution For The Quadratic Function F X X 2 2x 8 Find A The Axis Of Symmetry And The Vertex B The X Intercepts And Y Intercepts C The Domain And Range D

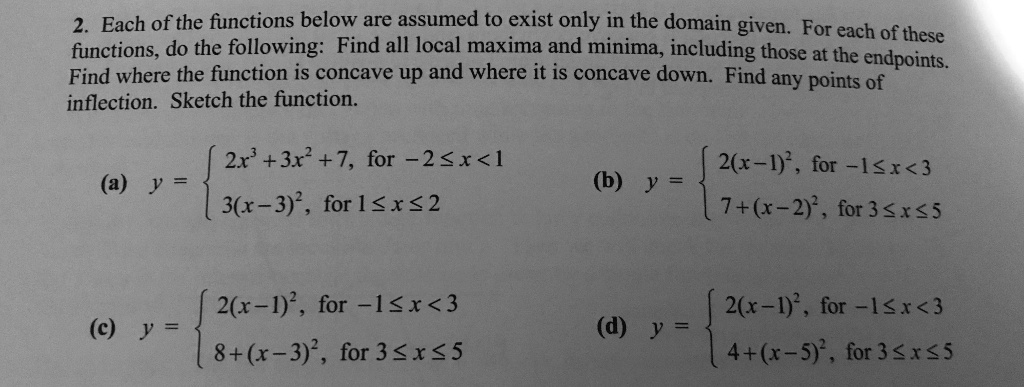
Each Of The Functions Below Are Assumed To Exist Only Itprospt

Answer (1 of 2) y= x² 8x 4 12 12 ( adding and subtracting 12) y= x² 8x 16 12 y= (x4)^2 12 Since the range of the square function is from 0 to infinity, the range of y is (Domain y= x/ (x^26x8) \square!Domain and range of polynomial, fractional, irrational and integral part functions

Exercise 1 3 Functions Problem Questions With Answer Solution

How To Find Domain And Range Of The Inverse Of A Relation Sat Math

Weekly Subscription $249 USD per week until cancelled Monthly Subscription $799 USD per month until cancelled Holidays Promotion Annual Subscription $1999 USD for 12 months (40% off)Option 1 Restrict the domain of q to x ≥ 0 so that the inverse will also be a function ( q − 1) The restriction x ≥ 0 on the domain of q will restrict the range of q − 1 such that y ≥ 0 q domain x ≥ 0 range y ≥ 0 q − 1 domain x ≥ 0 range y ≥ 0 or Option 2 Restrict the domain of q to x ≤ 0 so that the inverse willIf R = (X, Y) X, Y ∈ W, 2x Y = 8, Then Write the Domain and Range of R CBSE CBSE (Commerce) Class 11 Textbook Solutions Important Solutions 14 Question Bank Solutions 9274 Concept Notes & Videos 537 Syllabus Advertisement Remove all ads If R

4 13 Set Domain Graphing Calculator By Mathlab User Manual

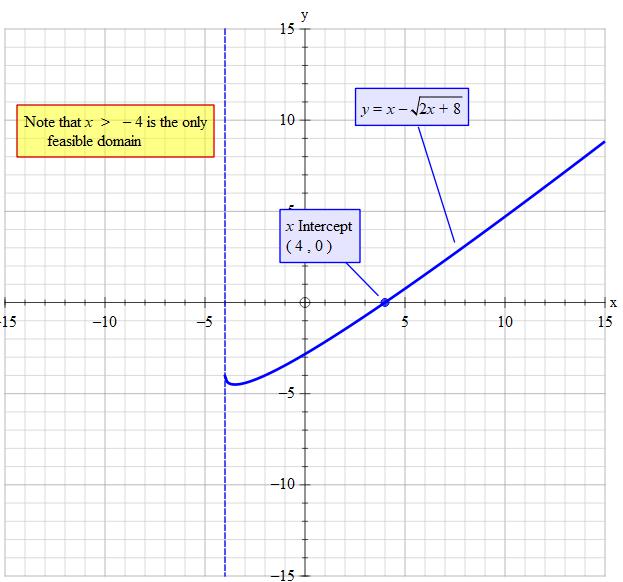
How Do You Solve Sqrt 2x 8 X Socratic

6 2x 8 x2 12 1 x x 6 (m) lim x!1 p x2 22 p x 1 (n) lim x!1 p x 2 x (o) lim x!7 6 p 2x 14 (p) lim x!1 p 3 3x (q) lim x!1 x4 10 4x3 x (r) lim x!1 3 r x 3 5 x (s) lim x!1 3x3 x2 2 x2 x 32x 1 a domain b holes c vertical asymptotes d horizontal asymptotes e yintercept f xintercepts 1 2 2 2 6 xx fx xx 2 2 2 Misc 3 Find the domain of the function "f" (x) = (" " 𝑥2 2𝑥 1)/(𝑥2 − 8𝑥 12) "f" (x) = (" " x2 2x 1)/(x2 − 8x 12) = (" " (x 1)2)/(x2 −2x Now domain refers to all the values of x for which y exists Here y will exist for all values of x that allow x^2 3x 2 to be positive as the logarithm for

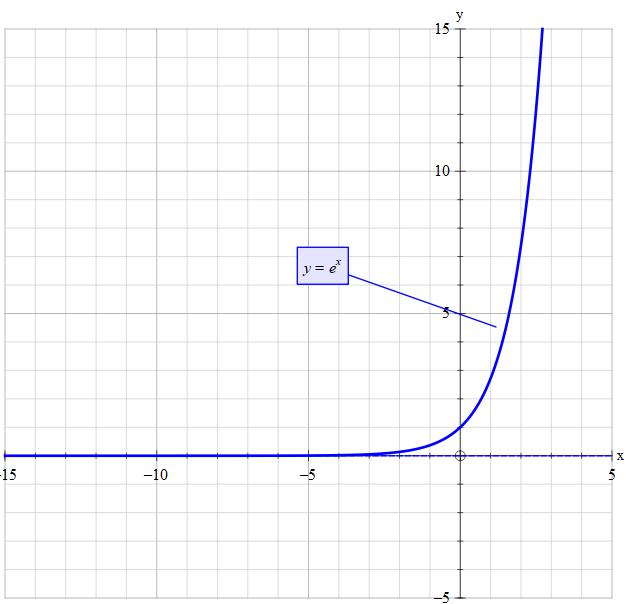
What Is The Domain And Range Of Y E X Socratic

Misc 3 Find Domain Of F X X2 2x 1 X2 8x 12

Inverse Function Questions and Answers Get help with your Inverse function homework Access the answers to hundreds of Inverse function questions that are explained in a way that's easy for you y=x^2 2x8 domain given that y = 2x & x , y ∈ n here, x is a always natural number, so, domain = set of natural numbers = n here, y is always an even number range = set of even natural numbers codomain = set of natural numbers = n here, the first elements (ie x) are not repeating hence they have unique (one) images (iey)1what is the area boundedFrom this chart, we see that the parabola y = x 2 contains the points (3, 9) and (4, 16) On the other hand, he parabola y = 2x 2 contains the points (3, 18) and (4, 32) On the first equation, y = x 2, to move horizontally across the xaxis from x = 3 to x = 4, we move up vertically on the yaxis from y = 9 to y = 16 which is 7 unitsSo, to go from the point (3, 9) to (4, 16), we move over 1

1 Write The Range For The Equation Shown Below If The Domain 1 2 3 4 5 Y 2x 2 A 0 2 4 6 8 B 0 2 4 6 8 C 4 6 8 10 12 Ppt Download

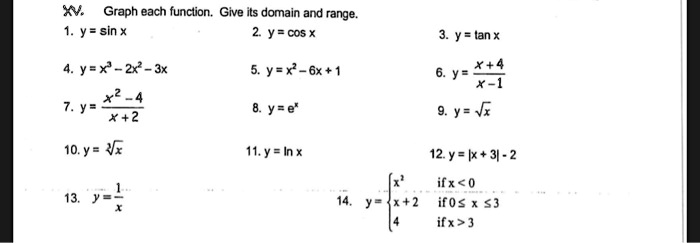
X Graph Each Funciion Give Its Domain And Range 1 Y Itprospt

Review for Exam 2 I Sections 131, 133 I 50 minutes I 5 problems, similar to homework problems I No calculators, no notes, no books, no phones I No green book needed Section 147 Example (a) Find all the critical points of f (x,y) = 12xy − 2x3 − 3y2 (b) For each critical point of f , determine whether f has a local Observe that when the function is positive, it is symmetric with respect to the equation $\mathbf{y = x}$Meanwhile, when the function is negative (ie, has a negative constant), it is symmetric with respect to the equation $\mathbf{y = x}$ Summary of reciprocal function definition and properties Before we try out some more problems that involve reciprocal2x^28=0 2x^2=8 x^2=4 x=2 horizontal asymptotes y=5/2 (when degree of numerator =degree of denominator, divide lead coefficient of numerator by lead coefficient of denominator) xintercept set y=0 numerator=0 5x^27x2=0 at x=1 and at x=04 yintercept set x=0 y=2/8=1/4 domain (∞,2) U (2,2) U (2,∞) range (∞,06) U (5

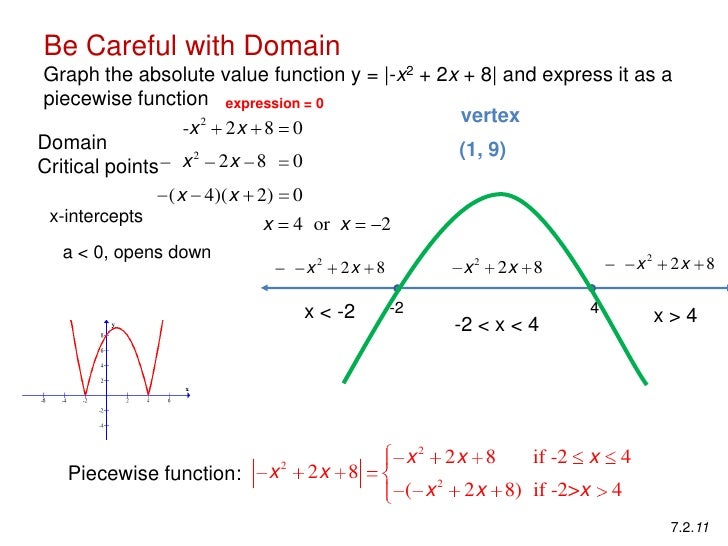
7 2 Abs Value Function

2x 8 The Rational Function F X X2 7x 12 Has A Horizontal Asymptote At Y Homeworklib

Easy as pi (e) Unlock StepbyStep Natural Language Math InputExample 2 Find the vertical and horizontal asymptotes of the graph of f(x) = 4x2 x2 8 Solution The vertical asymptotes will occur at those values of x for which the denominator is equal to zero x2 8 = 0 x2 = 8 x = p 8 Since p 8 is not a real number, the graph will have no vertical asymptotesExponential inequalities are inequalities in which one (or both) sides involve a variable exponent They are useful in situations involving repeated multiplication, especially when being compared to a constant value, such as in the case of interest For instance, exponential inequalities can be used to determine how long it will take to double ones money based on a certain rate of interest;

Restriction Mathematics Wikipedia

Graph The Quadratic Function Y X 2 2x 3 Vertex X Y Intercepts Symmetry Domain Range Youtube

Find the domain and the range after graphing y= x^2 1 Domain Start with the assumption that the domain is "all Real Numbers" Then look at your equation to see if certain forms there restrict the values of "x" Examples 1/(x2) which means xSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more3 x x (l) lim x!

How To Find Domain And Range From A Graph Video Khan Academy

Identifying Quadratic Functions Ppt Download

 Draw the graph for the relation R= {(x, y) y = 2x 1} Where both x and y are real numbers Solution The equation y = 2x 1 represents a straight line, this line passes throng uncountable points3 (a) f ( x) = 6 , g ) =3 (b) f(x 2, g(x) = 4x (c) f(x) = 2x, g(x) = x2 (d) f(x) = x4, g(x) = ex (e) f(x) = x1, g(x) = x2 4 (a) domain is all real x, range is −1 ≤ y ≤ 1 (b) domain is all real x, range is y ≥ 1 (c) domain is x < 0, range is all real y (d) domain is x 6= 0 , range isDefinition 33 Suppose f X → Y is a onetoone correspondence Then there is a function f−1 Y → X, called the inverse of f defined as follows f−1(y) = x ⇐⇒ f(x) = y Inverse functions are very important both in mathematics and in real world applications (eg population modeling, nuclear physics (half life problems) etc)

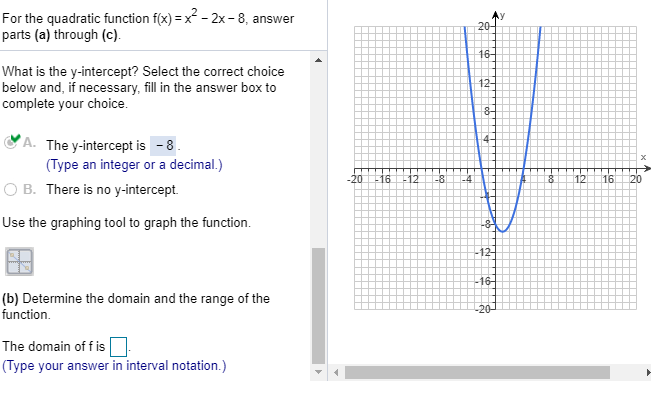
Solved For The Quadratic Function F X X2 2x 8 Answer Chegg Com

Solved X 2 X F X2 2x 8 Determine The Domain Determine The X Intercept S Determine The V Intercept Determine The Equation S For The Vertical Asymptote S Determine The Approximation Equation Near All X Intercepts Determine

3 For each solution ( x,y,z,,µ), find f(x,y,z) and compare the values you get The largest value corresponds to maximums, the smallest value corresponds to minimums 5 Examples Example 51 Use Lagrange multipliers to find the maximum and minimum values of the function subject to the given constraints xy z =0and x2 2z2 =1 f(x,y,z(2x)ey2 x2 (x2 y2)ey2 x2( 2x) = 0 The first thing that stands out to me is that both terms have an ey2 x2 Furthermore, eanything is never0 SoIcandividebothsidesbyey2 x2 andbedonewithit!The domain of definition of the function 7 − x P x − 3 , is Medium View solution > The domain of definition of the function f ( x) given by the equation 2 x

Ex 2 2 2 Define Relation R On Set N Of Natural Numbers

Example 10 R X Y Y 2x What Is Domain Codomain Range

2 x−4 2x0 −2x8 8 Thus, 2x x−4 = 2 8 x−4, and the right hand side of this equality is in the desired form mentioned above the q(x) is 2, r(x) is 8, and d(x) is x−4 So, the line y = 2 is a horizontal asymptote Lastly, we find the domain Recalling that the domain of a rational function is all real numbers exceptStick with those, and you will have a polynomial All polynomials have a domain of "All Real Numbers" In interval notation, we write #(\infty,\infty)#Given g(x)= \dfrac{x2}{x^24} Find the domain, range, x and yintercepts, and the vertical and horizontal asymptotes of the function g(x), and sketch the graph View Answer Suppose x is a

Domain

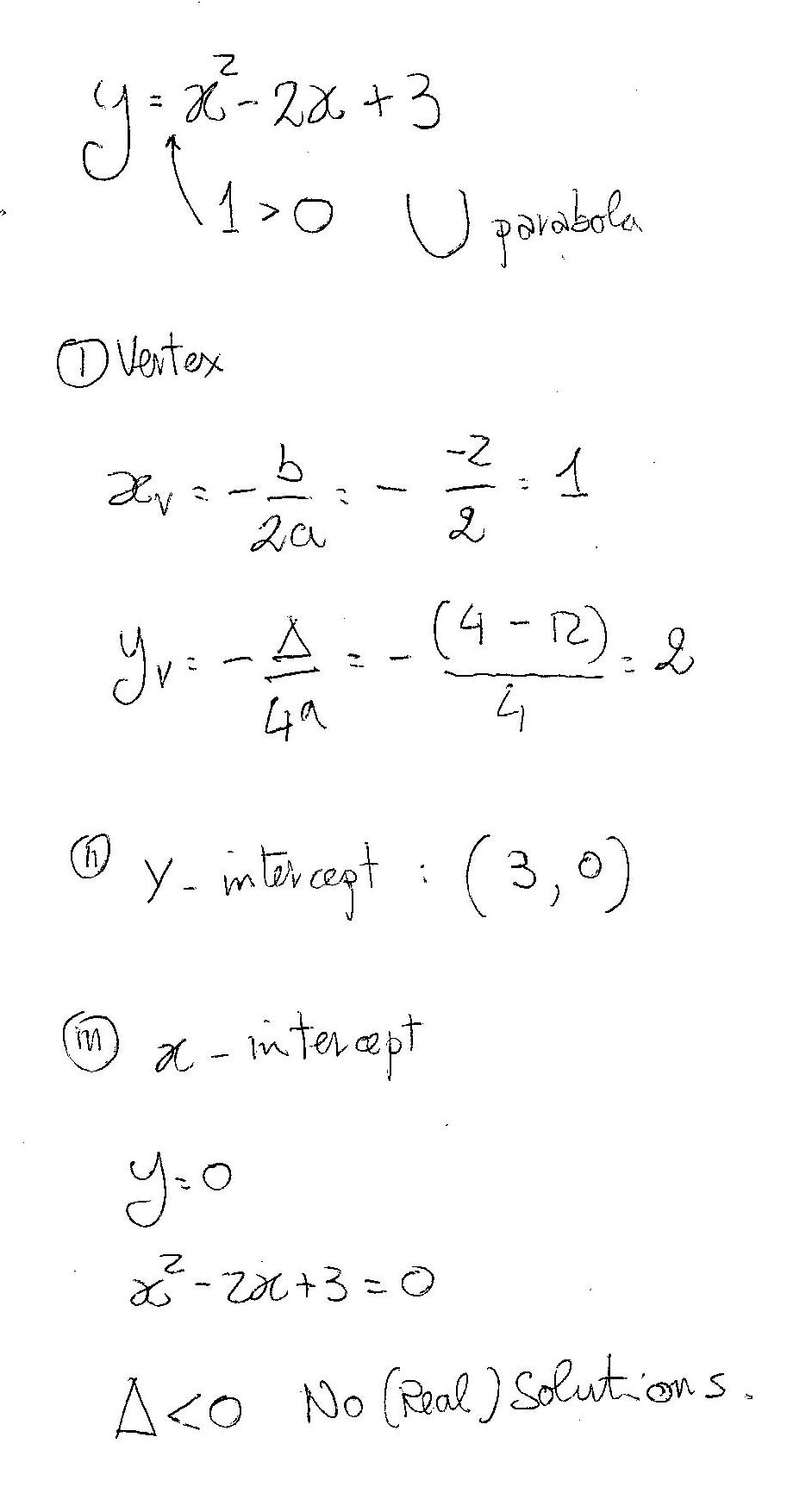
How Do You Graph Y X 2 2x 3 Socratic

Algebra Calculator is a calculator that gives stepbystep help on algebra problems See More Examples » x3=5 1/3 1/4 y=x^21 Disclaimer This calculator is not perfect Please use at your own risk, and please alert us if something isn't working Thank youDomain and range of z = x^2 y^2 WolframAlpha Area of a circle?Textbook Exercise 51 On separate axes, accurately draw each of the following functions Use tables of values if necessary Use graph paper if available \ (y_1 = x^2\) \ (y_2 = \frac {1} {2}x^2\) \ (y_3 = x^2 1\) \ (y_4 = 2x^2 4\) Use your sketches of the functions given above to complete the following table (the first column has been

Find The Range Of The Expression Y X 2 2x 8 X 2 4x 5 Forall Permissible Value Of X

In Problems 1 8 Find The Domain And Range Ofthe Funct Itprospt

 Contoh, g x x 2 2x, dibaca fungsi g memetakan x ke x 2 2x Bentuk penyebutan lain yang ekuivalen adalah g(x) = x 2 2x dan y = x 2 2x Lalu bagaimana cara menentukan domain dan range suatu fungsi?Y= e2x1 (horizontal compression 2 times) y = 3e2x1 ( vertical stretch 3 times) Example Solve x x 4 2 2 (i) Rewrite the equation in the form au = av Since 4 = 22, we can rewrite the equation as 2 x 2 2 Using properties of exponents we get 2x22 x (ii) Use property 8 of exponential functions to conclude that u = vThe Parabola Given a quadratic function f ( x) = a x 2 b x c, it is described by its curve y = a x 2 b x c This type of curve is known as a parabola A typical parabola is shown here Parabola, with equation y = x 2 − 4 x 5

Misc 6 Let F X X2 1 X2 X R Find Range Chapter 2

Solved The Following Function Is Given Answer The Following Chegg Com

Warm Up Exercises 1 Make A Table For Y 2x 3 With Domain 0 3 6 And Write A Rule For The Function Answer Y 3x 1 X0369 Y Input X Ppt Download

How To Find The Domain And Range From Y X 2 2x 8 Quora

D Domain And Range

Example 21 Find Domain Of F X X2 3x 5 X2 5x 4

Inverse Functions Domain Range With Fractions Square Roots Graphs Youtube

Discontinuity Calculator Wolfram Alpha

Chapter 1 Practice Exercises

Oneclass Sketch The Graph Of Y X 8 2x 22 2x Given That Cm 3 Is The Volume Of A Cuboid With H

X2 2x 8 Solution

Results For The Two Segments Domain The Contour Lines Of The Function Download Scientific Diagram

Tentukan Domain Dan Range Dari Fungsi F X X 2 X 2x 8 Adalah Brainly Co Id

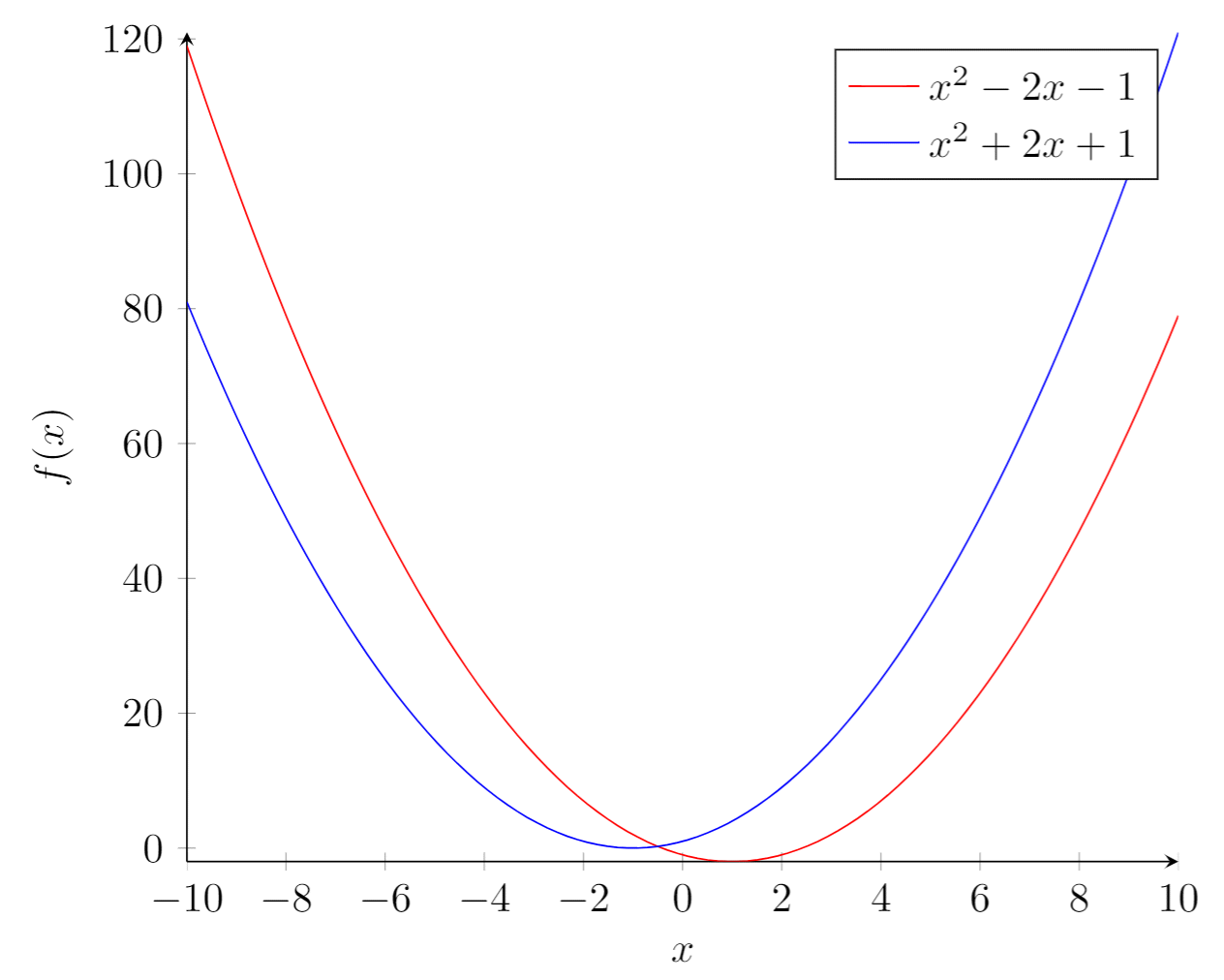
Pgfplots Package Overleaf Online Latex Editor

Which Model Shows The Correct Factorization Of X2 2x 8 Knowme Live

Solved In Problems 1 8 Find The Domain And Range Of The Chegg Com

Find Domain And Range Of Function Y 1 X 2 Youtube

Domain And Range Of 1 X 2 2x 8 Youtube

Draw The Graph Of Polynomial F X X 2 2x 8 Brainly In

Diketahui Fungsi Kuadrat Fx X2 2x 8 Tentukan I Gauthmath

Identify Quad Parts Projectile Motion Pdf Motion Physics Physics

How To Find The Domain Of A Function Video Khan Academy

A Graph And Determine The Range Domain Vertex A Gauthmath

File Y X 2 2x Svg Wikimedia Commons

How To Find The Domain And Range From Y X 2 2x 8 Quora

10 Write This Equation In Standard Form Y X 8r 9 J Itprospt

Ex 2 2 6 Determine Domain And Range Of R X X 5

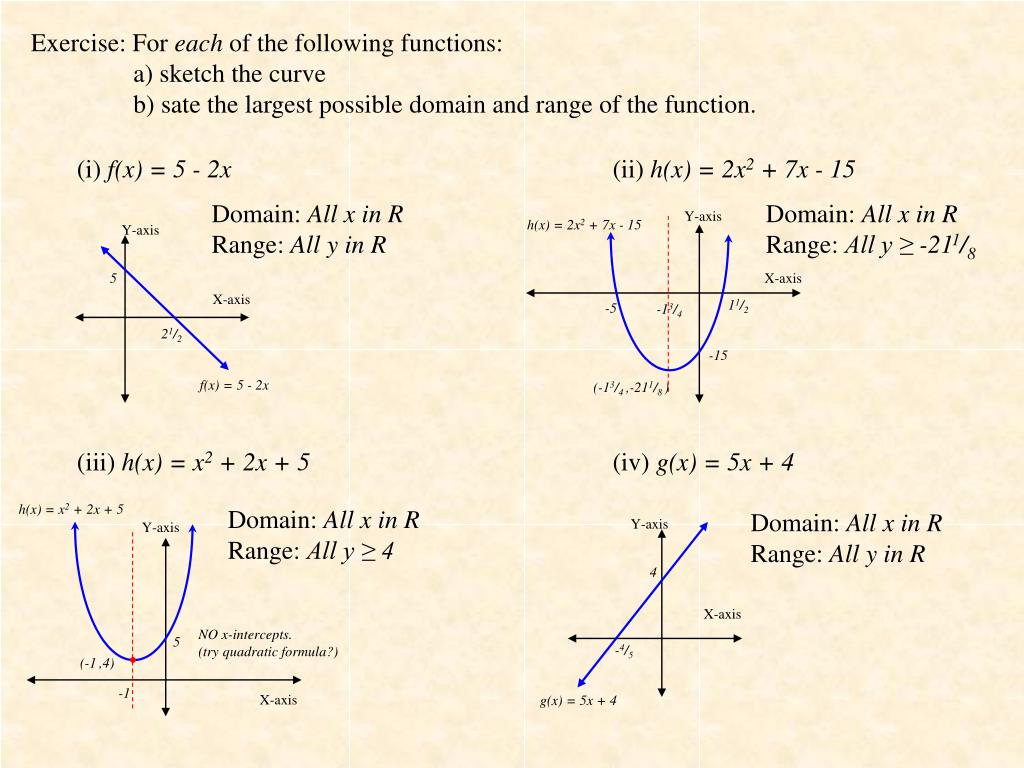
Ppt Function Iii Powerpoint Presentation Free Download Id

How To Find The

If The Function F X Has A Domain Of 2 X 8 And A Range Of 4 Y 6 And The Function G X Is Defined By The Formula G X 5f 2x Then What Are

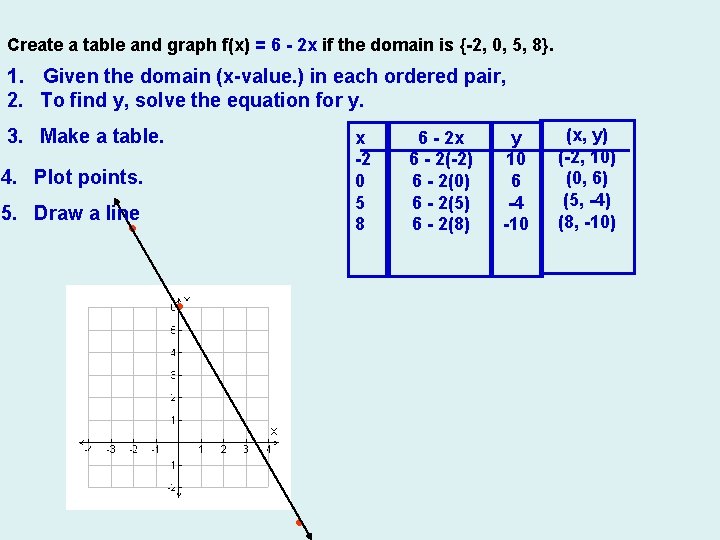
Graph The Linear Equation Yx 2 1 Draw

Solution How To Graph A Parabola Using Y X2 2x 8

Solved Find The Following Function Statc Thc Following 2r 8 26 4 26r 2 2 3 F X X 21 8 X 2r 8 R 4 R 2 A X Intcrccpt S B Y Intercepl C Domain D Vertical Asymptote S

How To Find The Domain And Range From Y X 2 2x 8 Quora

How To Find The Domain And Range From Y X 2 2x 8 Quora

Solution Graph The Function And State The Domain And Range G X X 2 2x 15 Can You Please Also Show The Graph

Question 8 4 Points Listen Find The Domain And The Ra Math

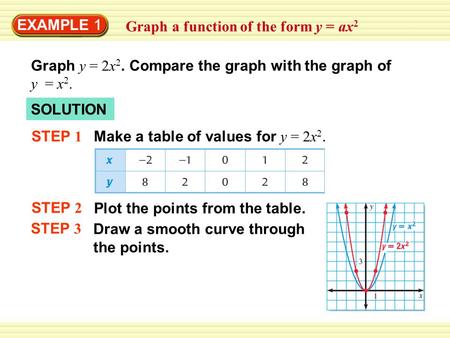
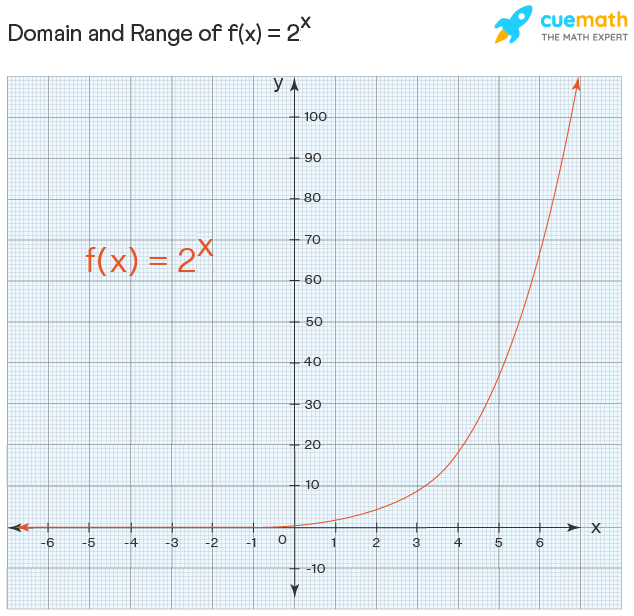
Example 2 Graph An Exponential Function Graph The Function Y 2 X Identify Its Domain And Range Solution Step 1 Make A Table By Choosing A Few Values Ppt Download

Solved A Determine The Domain Of Each Of The Functions Chegg Com

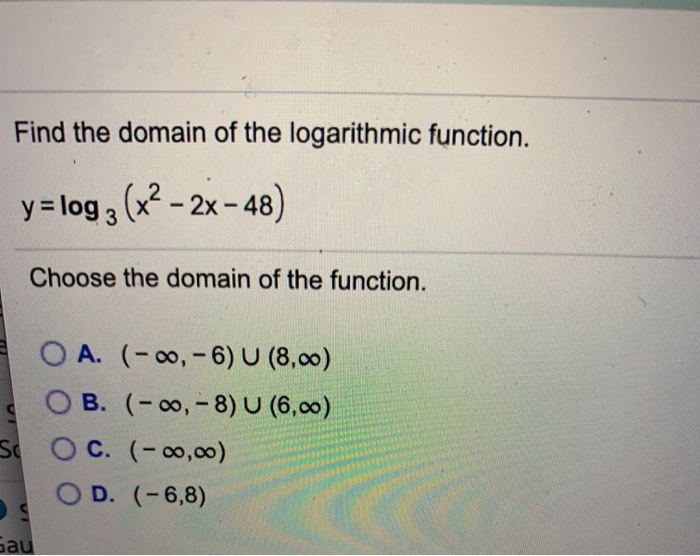
Solved Find The Domain Of The Logarithmic Function Y Log2 Chegg Com

Solved Answer The Following Questions For The Function F X Chegg Com

Name Algebra 2 Exam Review Part 2 December 15 All Correct

Identify The Domain And Range Of The Rational Function Math

Solved Find The Value For The Function X2 8 1 Find Ffx1 Chegg Com

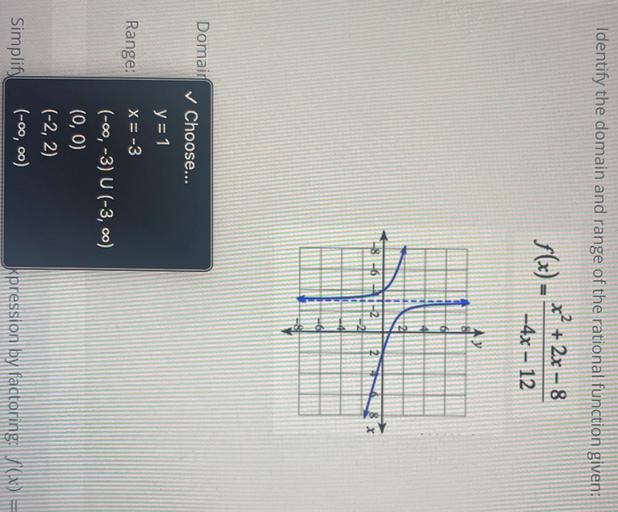
Identify The Domain And Range Of The Rational Function Math

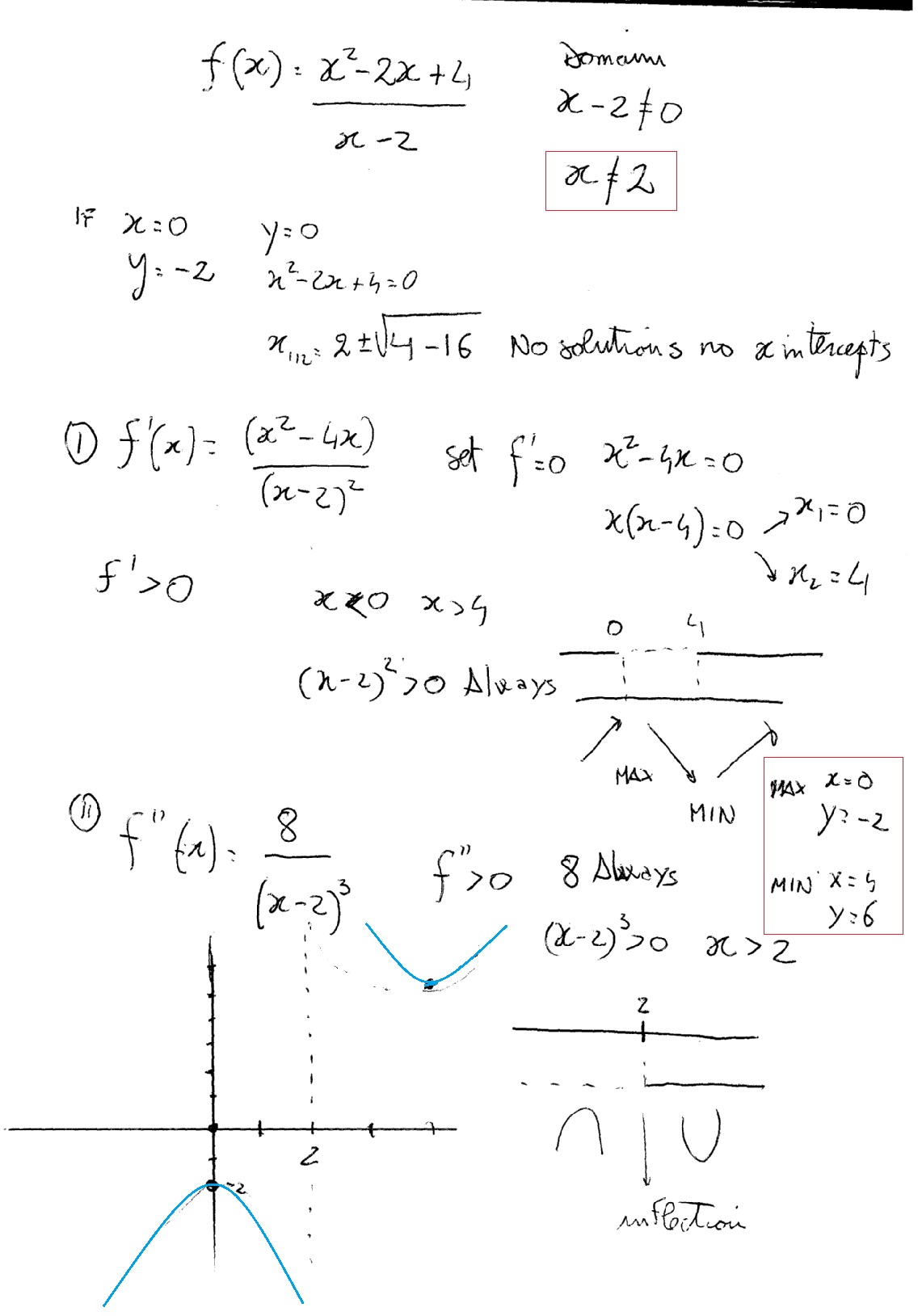
F X X 2 2x 4 X 2 F X X 2 4x X 2 2 F X 8 X 2 3 How To Find The Domain Of F X X And Y Intercepts Vertical Asymptotes The Critical Numbers Concave Up And Down And Sketch Graph Socratic

6 Ways To Find The Domain Of A Function Wikihow

Instantcert Credit College Algebra Lesson 22

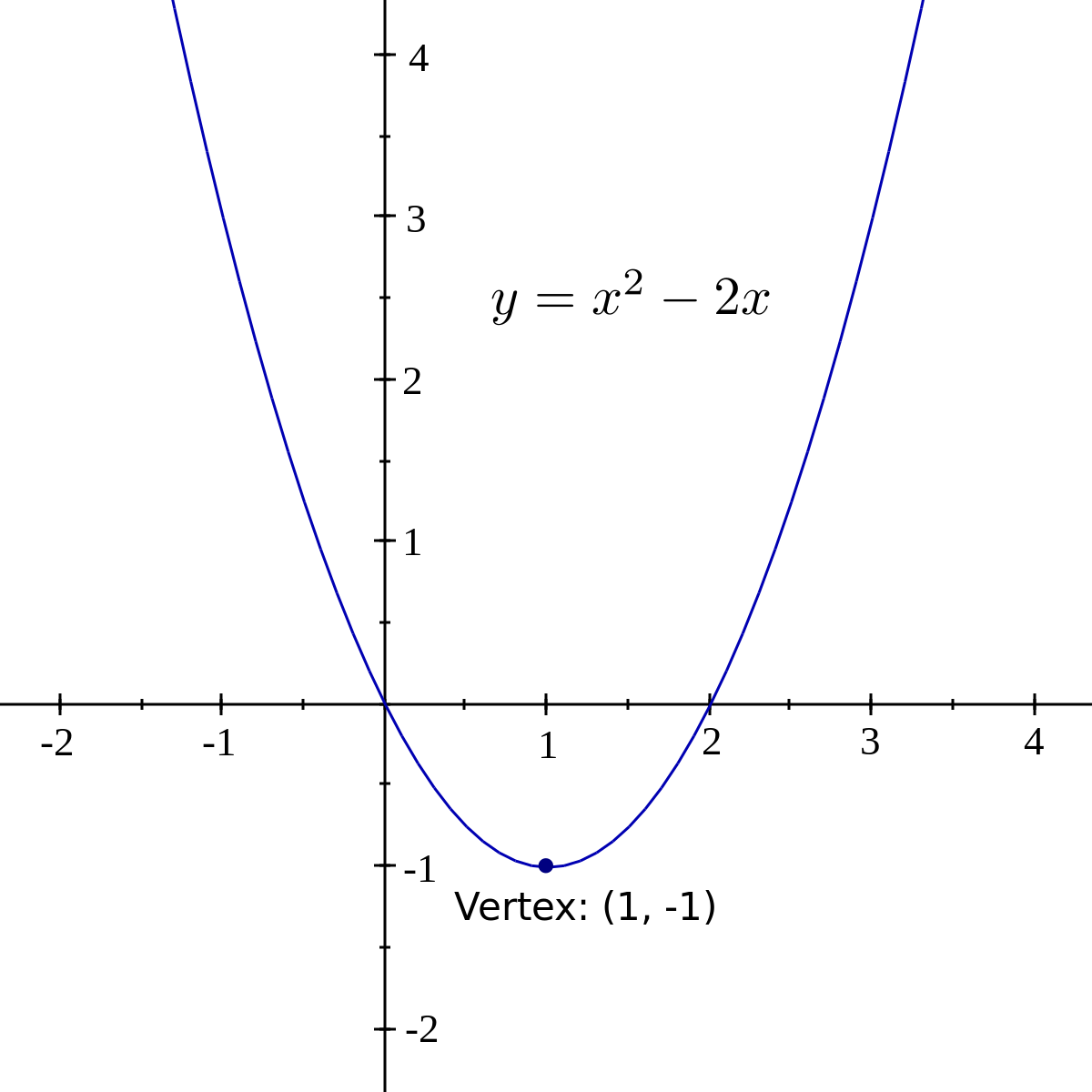
File Y X 2 2x Svg Wikimedia Commons

How To Find The Domain And Range From Y X 2 2x 8 Quora

How To Find The Domain And Range From Y X 2 2x 8 Quora

Solved 4 Pt 3 A Graph Yx 2 B State The Domain And The Chegg Com

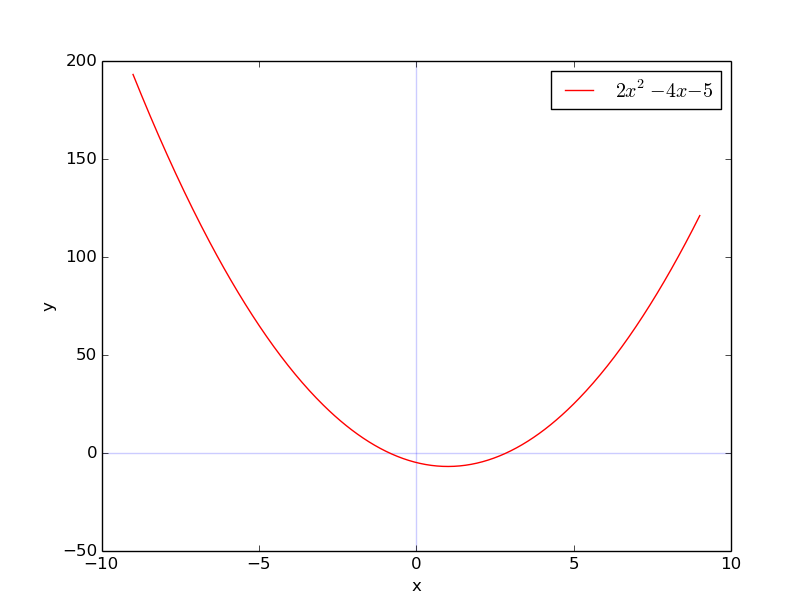
How Do You Find The Domain And Range Of Y 2x 2 4x 5 Socratic

Misc 3 Find Domain Of F X X2 2x 1 X2 8x 12

How To Graph Y Sqrt X Video Lesson Transcript Study Com

How To Find The Domain And Range From Y X 2 2x 8 Quora

The Domain Of The Function F X Sqrt Log 0 3 X 1 Sqrt X 2 2x 8 Is

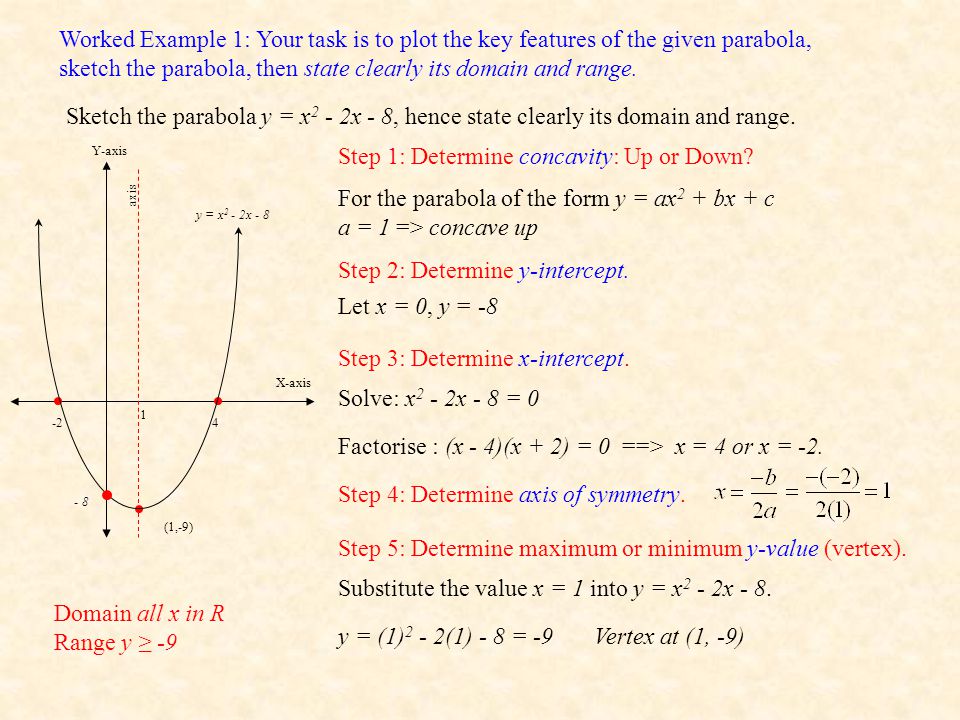
Functions Domain And Range By Mr Porter Ppt Download

How To Find The Domain And Range From Y X 2 2x 8 Quora

Lotus Domain Proteins Developmental Effectors From A Molecular Perspective

6 Ways To Find The Domain Of A Function Wikihow

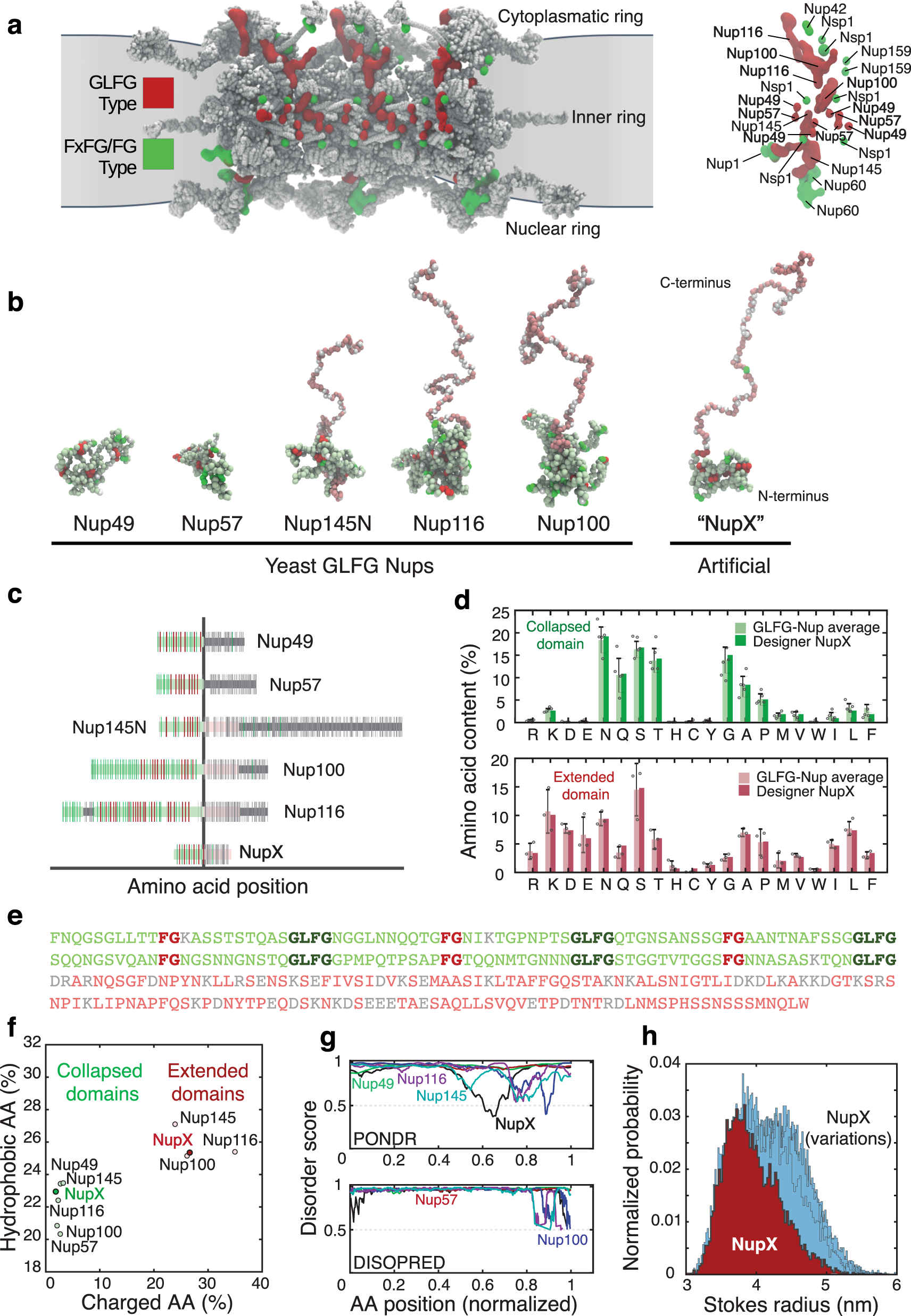
A Designer Fg Nup That Reconstitutes The Selective Transport Barrier Of The Nuclear Pore Complex Nature Communications

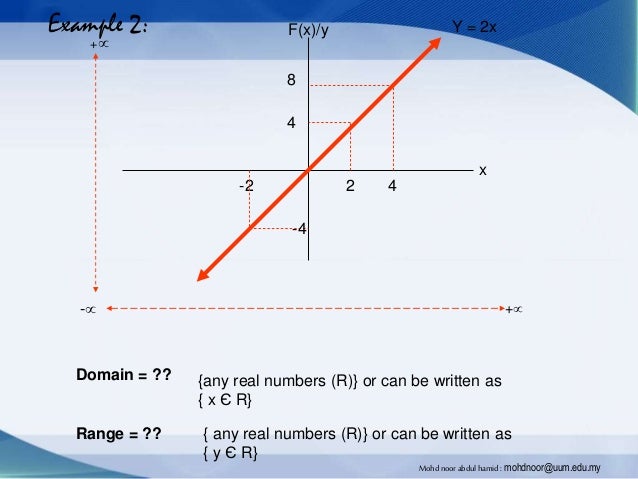
Introduction To Function Domain And Range Mohd Noor

Chapter 5 Inverse Functions And Applications Section Ppt Download

Solution State The Domain And Range Of The Function F X X Squared 3

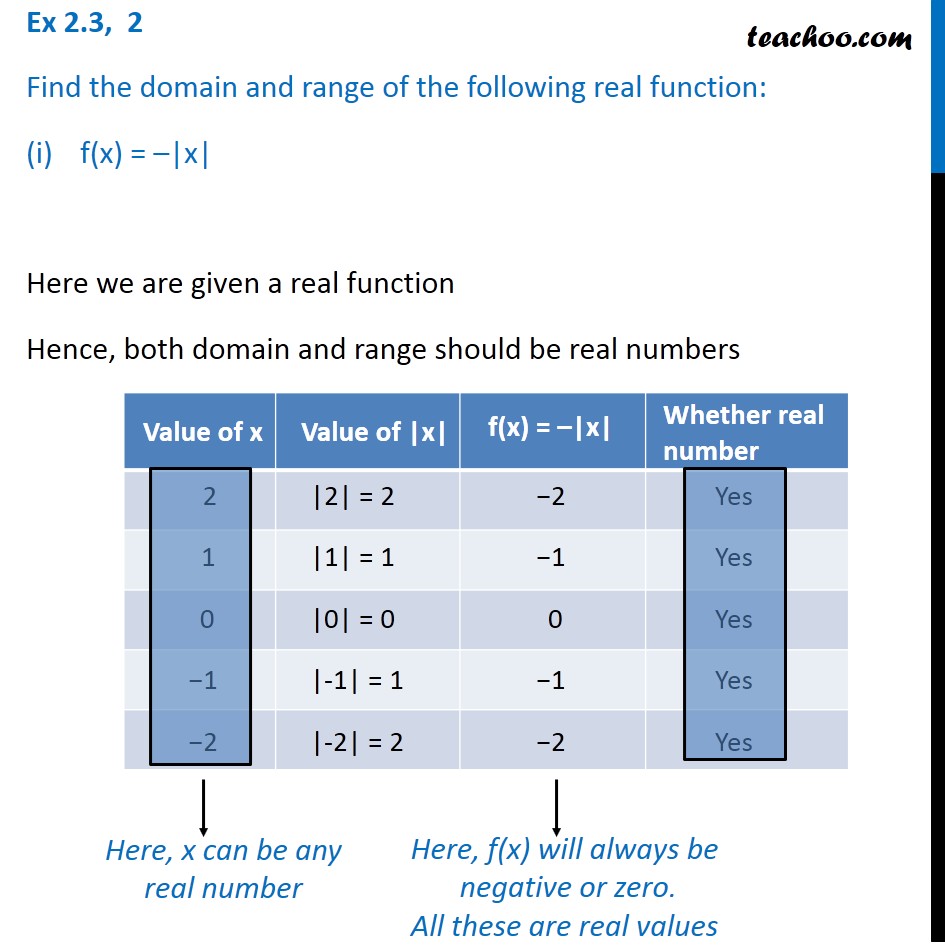
Ex 2 3 2 Find The Domain And Range Of The Function F X X

How To Find The Domain And Range From Y X 2 2x 8 Quora

Line Of Symmetry Parabolas Have A Symmetric Property To Them If We Drew A Line Down The Middle Of The Parabola We Could Fold The Parabola In Half We Ppt Download

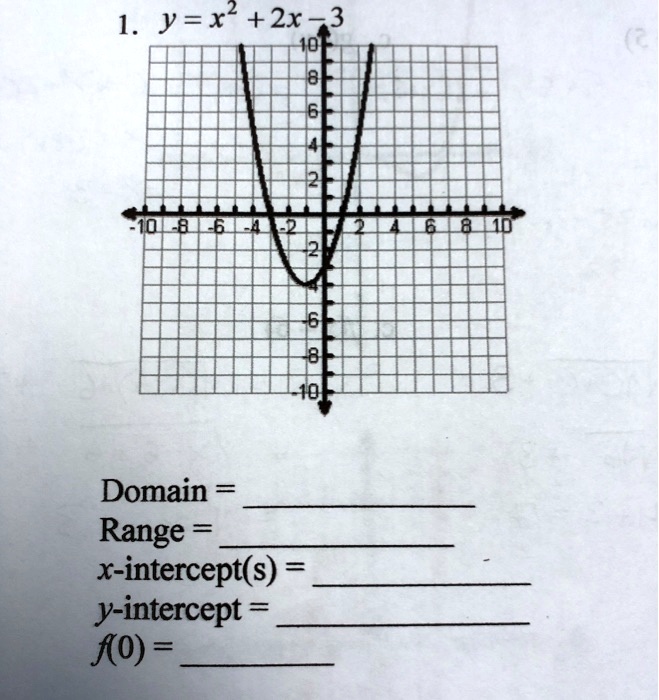
1 Y X 2 3domain Range X Intercept S Y Intercept Ko Itprospt

Solution Find The Minimum Value Of The Quadratic Y 2x 2 8x 8 At What X Value Does The Minimum Occur State The Domain And Range Of This Function Thank You

1

Functions Domain And Range By Mr Porter Ppt Download

C3 Functions

Which Polynomial Is Prime X2 X 1 X2 X 2 X2 1 Gauthmath

Maths Higher Homework Pg 224 Qs 10 13 23 26 Then To Do Past

Solved Find The Domain Of The Functions Given In The Problem Chegg Com

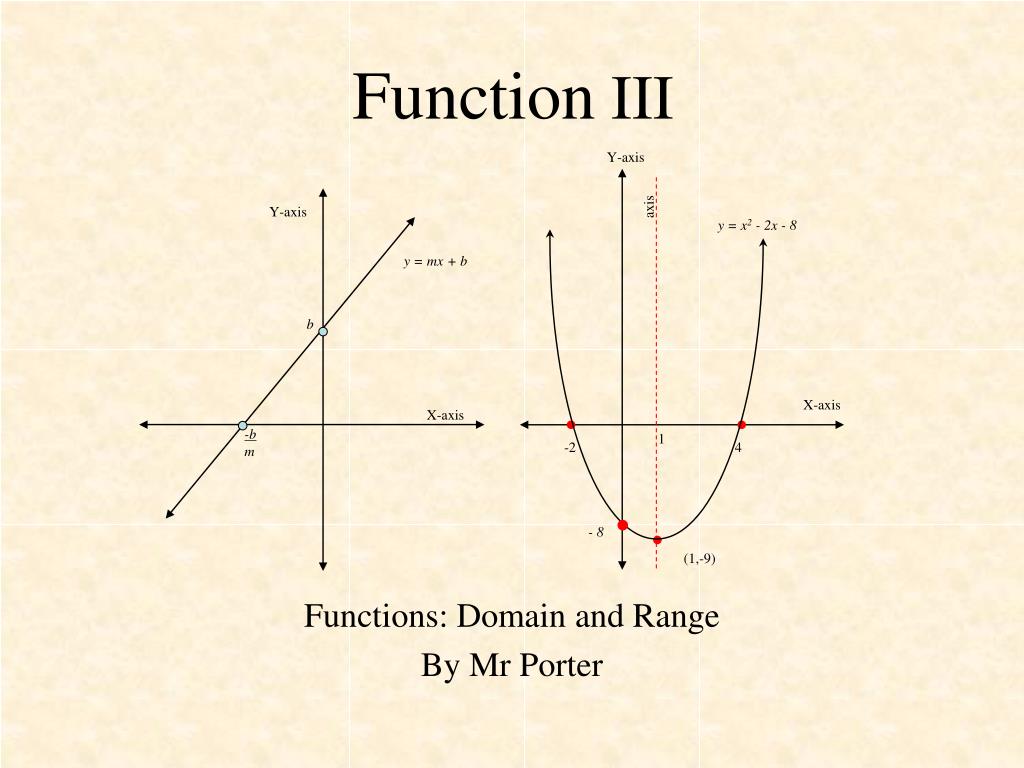
Ppt Function Iii Powerpoint Presentation Free Download Id

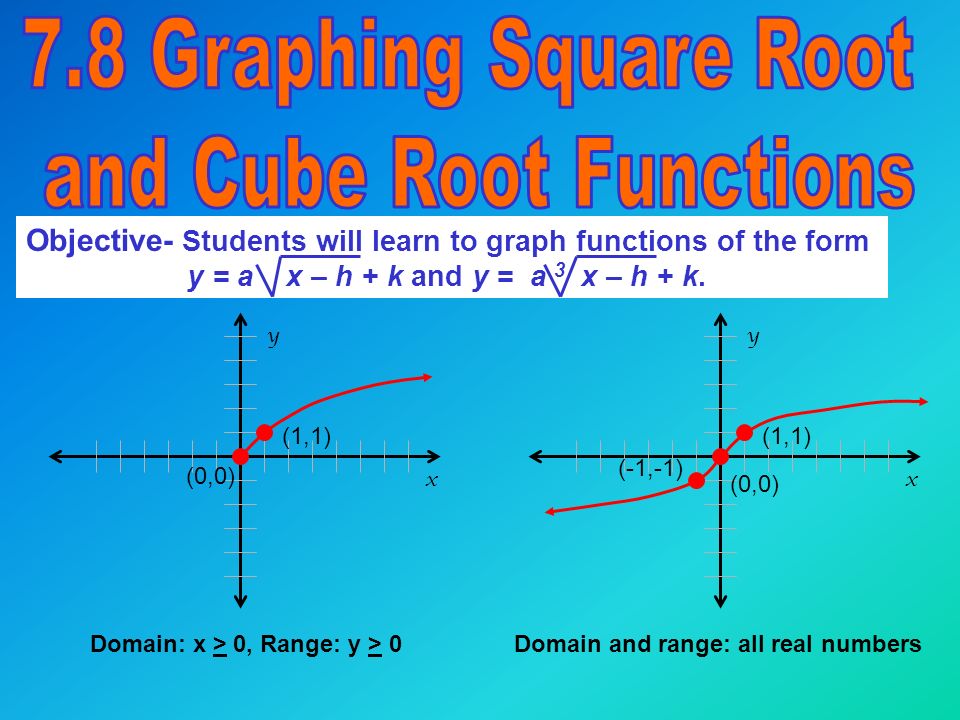
1 Identify The Domain And Range Inputoutput Graph Y 2x Domain 1 2 5 6 Range 2 Ppt Download

Incoming Term: y=x^2+2x-8 domain, domain and range of y=x^2-2x-8,